Pruebas de Merkle para la integridad de los datos fuera de línea

Introducción

Idóneamente, nos gustaría guardar todo en el almacenamiento de Ethereum, el cual se guarda en miles de computadoras y tiene una disponibilidad extremadamente alta (los datos no pueden ser censurados) e integridad (los datos no pueden ser modificados de una manera no autorizada), sin embargo almacenar una palabra de 32 bytes suele costar 20.000 gas. En el momento de redactar este artículo, el coste actual es de 6,60 $. A 21 centavos por byte esto es demasiado costoso para muchos usos.

Para resolver este problema, el ecosistema de Ethereum desarrolló muchas maneras alternativas de almacenar datos de forma descentralizada. Usualmente involucran compensar entre disponibilidad y precio. Sin embargo, normalmente se asegura la integridad.

En este artículo aprenderá cómo garantizar la integridad de los datos sin almacenarlos en la blockchain, utilizando pruebas de Merkleopens in a new tab.

¿Cómo funciona?

En teoría, podríamos almacenar simplemente el hash de los datos on-chain y enviar todos los datos en las transacciones que lo requieran. No obstante, sigue siendo demasiado caro. Un byte de data a una transacción cuesta alrededor de 16 gas, actualmente cerca de medio centavo, o aproximadamente 5 dólares por kilobyte. A 5.000 $ por megabyte, esto sigue siendo demasiado caro para muchos usos, incluso sin el coste añadido de acelerar los datos.

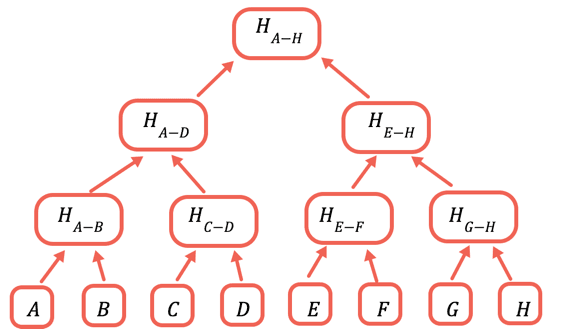
La solución consiste en acelerar repetidamente diferentes subconjuntos de los datos, de forma que para los datos que no necesite enviar, pueda simplemente enviar un hash. Esto se hace utilizando un árbol Merkle, una estructura de datos en arbol donde cada nodo es un hash de los nodos debajo:

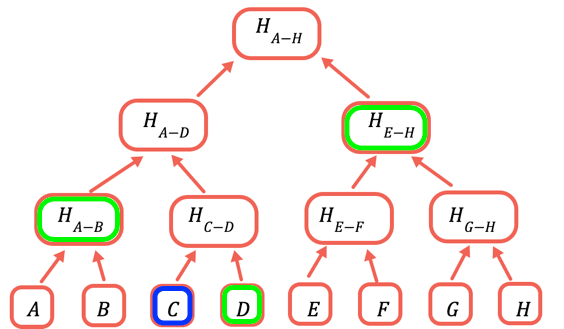
El hash raíz es la única parte que necesita almacenarse en la cadena. Para demostrar un determinado valor, proporcione todos los hash que necesitan combinarse con él para obtener la raíz. Por ejemplo, para probar C proporcione D, H(A-B) y H(E-H).

Implementación

El código de ejemplo se proporciona aquíopens in a new tab.

Código off-chain

En este artículo usamos JavaScript para los cálculos fuera de la cadena. La mayoría de las aplicaciones descentralizadas tienen su componente off-chain en JavaScript.

Creando la raíz de Merkle

Primero necesitamos proporcionar la raíz de Merkle a la cadena.

1const ethers = require("ethers")

Usamos la función hash del paquete ethersopens in a new tab.

1// The raw data whose integrity we have to verify. The first two bytes a
2// are a user identifier, and the last two bytes the amount of tokens the
3// user owns at present.
4const dataArray = [
5  0x0bad0010, 0x60a70020, 0xbeef0030, 0xdead0040, 0xca110050, 0x0e660060,
6  0xface0070, 0xbad00080, 0x060d0091,
7]

Codificar cada entrada en un único entero de 256 bits resulta en un código menos legible que el de JSON, por ejemplo. Sin embargo, esto significa un procesamiento significativamente menor para recuperar los datos en el contrato, unos costes de gas mucho menores. Se puede leer JSON on-chainopens in a new tab, pero es una mala idea si se puede evitar.

1// The array of hash values, as BigInts
2const hashArray = dataArray

En este caso para empezar nuestros datos son valores de 256 bits, por que no se necesita ningún procesamiento. Si utilizamos una estructura de datos más compleja, como cadenas, necesitamos asegurarnos de que hacemos hash los datos primero para obtener una matriz de hashes. Tenga en cuenta que esto también es porque no nos importa que los usuarios conozcan la información de otros usuarios. De lo contrario, habríamos tenido que hacer hash para que el usuario 1 no sepa el valor para el usuario 0, el usuario 2 no sabrá el valor del usuario 3, etc.

1// Convert between the string the hash function expects and the
2// BigInt we use everywhere else.
3const hash = (x) =>
4  BigInt(ethers.utils.keccak256("0x" + x.toString(16).padStart(64, 0)))

La función hash de ethers espera recibir una cadena en formato hexadecimal, por ejemplo 0x60A7, y responde con otra cadena con la misma estructura. Sin embargo, para el resto del código es más fácil usar BigInt, por lo que convertimos entre una cadena hexadecimal y viceversa.

1// Symmetrical hash of a pair so we won't care if the order is reversed.
2const pairHash = (a, b) => hash(hash(a) ^ hash(b))

Esta función es simétrica (hash de un xoropens in a new tab b). Esto significa que cuando revisamos la prueba de Merkle no debemos preocuparnos sobre si el valor de la prueba debe ser colocado antes o después del valor calculado. La verificación de pruebas de Merkle se realiza on-chain, así que mientras menos operaciones sean necesarias allí, mejor.

Advertencia: la criptografía es más complicada de lo que parece. La versión inicial de este artículo tenía la función hash hash(a^b). Eso era una mala idea porque significaba que, si conocías los valores legítimos de a y b, podrías usar b' = a^b^a' para probar cualquier valor a' que quisieras. Con esta función, tendría que calcular b' de modo que hash(a') ^ hash(b') sea igual a un valor conocido (la siguiente rama hacia la raíz), lo cual es mucho más difícil.

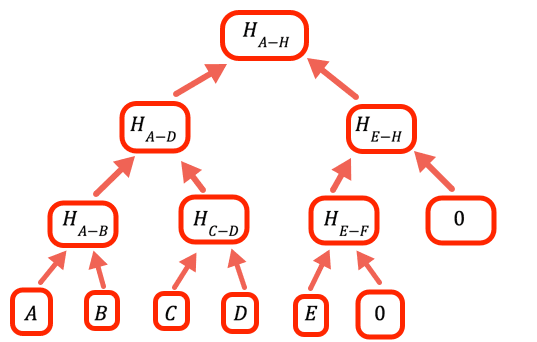
1// The value to denote that a certain branch is empty, doesn't
2// have a value
3const empty = 0n

Cuando el número de valores no es un entero potencia de dos, necesitamos manejar ramas vacías. La manera en que este programa lo hace es colocando cero como marcador de posición.

1// Calculate one level up the tree of a hash array by taking the hash of
2// each pair in sequence
3const oneLevelUp = (inputArray) => {
4  var result = []
5  var inp = [...inputArray] // To avoid over writing the input // Add an empty value if necessary (we need all the leaves to be // paired)
6
7  if (inp.length % 2 === 1) inp.push(empty)
8
9  for (var i = 0; i < inp.length; i += 2)
10    result.push(pairHash(inp[i], inp[i + 1]))
11
12  return result
13} // oneLevelUp
Mostrar todo

La función «escala» un nivel en el árbol Merkle al hacer hash de los pares de valores en la capa actual. Tenga en cuenta que esta no es la implementación más eficiente; pudimos haber evitado copiar el input y solo añadir hashEmpty cuando corresponda en el ciclo, pero este código está optimizado para la legibilidad.

1const getMerkleRoot = (inputArray) => {
2  var result
3
4  result = [...inputArray] // Climb up the tree until there is only one value, that is the // root. // // If a layer has an odd number of entries the // code in oneLevelUp adds an empty value, so if we have, for example, // 10 leaves we'll have 5 branches in the second layer, 3 // branches in the third, 2 in the fourth and the root is the fifth
5
6  while (result.length > 1) result = oneLevelUp(result)
7
8  return result[0]
9}
Mostrar todo

Para obtener la raíz, escalamos hasta que solo quede un valor.

Creando una prueba de Merkle

Una prueba de Merkle son los valores que se mezclan junto con el valor que se demuestra para recuperar la raíz de Merkle. Por lo general, el valor para probar está disponible a partir de otros datos, por eso prefiero proporcionarlo de manera separada, en vez de como una parte del código.

1// A merkle proof consists of the value of the list of entries to
2// hash with. Because we use a symmetrical hash function, we don't
3// need the item's location to verify the proof, only to create it
4const getMerkleProof = (inputArray, n) => {
5    var result = [], currentLayer = [...inputArray], currentN = n
6
7    // Until we reach the top
8    while (currentLayer.length > 1) {
9        // No odd length layers
10        if (currentLayer.length % 2)
11            currentLayer.push(empty)
12
13        result.push(currentN % 2
14               // If currentN is odd, add with the value before it to the proof
15            ? currentLayer[currentN-1]
16               // If it is even, add the value after it
17            : currentLayer[currentN+1])
18
Mostrar todo

Hasheamos (v[0],v[1]), (v[2],v[3]), etc. Encontes, para valores pares necesitamos el siguiente, y para valores impares, el anterior.

1        // Move to the next layer up
2        currentN = Math.floor(currentN/2)
3        currentLayer = oneLevelUp(currentLayer)
4    }   // while currentLayer.length > 1
5
6    return result
7}   // getMerkleProof

Código on-chain

Por último, tenemos el código que comprueba la prueba. El código on-chain está escrito en Solidityopens in a new tab. La optimización es más importante aquí porque el gas es relativamente caro.

1//SPDX-License-Identifier: Public Domain
2pragma solidity ^0.8.0;
3
4import "hardhat/console.sol";
Copiar

Escribí esto usando el entorno de desarrollo Hardhatopens in a new tab, que nos permite tener salidas en consola desde Solidityopens in a new tab durante el desarrollo.

1
2contract MerkleProof {
3    uint merkleRoot;
4
5    function getRoot() public view returns (uint) {
6      return merkleRoot;
7    }
8
9    // Extremely insecure, in production code access to
10    // this function MUST BE strictly limited, probably to an
11    // owner
12    function setRoot(uint _merkleRoot) external {
13      merkleRoot = _merkleRoot;
14    }   // setRoot
Mostrar todo
Copiar

Establecer y obtener funciones para la raíz de Merkle. Permitir que cualquier persona actualice la raíz de Merkle es una muy mala idea en un sistema en producción. Aquí lo hago con el objetivo de la simplicidad en el código de ejemplo. No lo haga en un sistema donde la integridad de los datos realmente importe.

1    function hash(uint _a) internal pure returns(uint) {
2      return uint(keccak256(abi.encode(_a)));
3    }
4
5    function pairHash(uint _a, uint _b) internal pure returns(uint) {
6      return hash(hash(_a) ^ hash(_b));
7    }
Copiar

Esta función genera un par hash. Es simplemente la traducción a Solidity del código JavaScript para hash y pairHash.

Nota: Este es otro caso donde se priorizó la legibilidad sobre la eficiencia. Según la definición de la funciónopens in a new tab, podría ser posible almacenar los datos como un valor bytes32opens in a new tab y evitar conversiones.

1    // Verify a Merkle proof
2    function verifyProof(uint _value, uint[] calldata _proof)
3        public view returns (bool) {
4      uint temp = _value;
5      uint i;
6
7      for(i=0; i<_proof.length; i++) {
8        temp = pairHash(temp, _proof[i]);
9      }
10
11      return temp == merkleRoot;
12    }
13
14}  // MarkleProof
Mostrar todo
Copiar

En notación matemática, la verificación de pruebas de Merkle se ve así: H(proof_n, H(proof_n-1, H(proof_n-2, ... H(proof_1, H(proof_0, value))...))). Este código lo implementa.

Las pruebas de Merkle y los rollups no se mezclan

Las pruebas de Merkle no funcionan bien con los rollups. La razón es que los rollups escriben todos los datos de la transacción en L1, pero los procesa en L2. El costo de enviar una prueba de Merkle con una transacción se promedia en 638 de gas por capa (actualmente, un byte en un llamado de datos cuesta 16 de gas si es diferente a cero y 4 si es cero). Si tenemos 1024 palabras de datos, una prueba de Merkle requiere diez capas o un total de 6380 de gas.

Por ejemplo, mirando Optimismopens in a new tab, el gas en L1 cuesta unos 100 gwei, mientras que el gas en L2 cuesta 0.001 gwei (ese es el precio normal, aunque puede subir con congestión). Entonces para el coste de un gas L1 podemos gastar mil de gas en L2. Asumiendo que no hemos sobrescrito el almacenamiento, esto significa que podemos escribir alrededor de cinco palabras en el almacenamiento en L2 para el precio de un gas L1. Para una sola prueba de Merkle, podemos escribir todas las 1024 palabras en almacenamiento (suponiendo que pueden calcularse on-chain en vez de ser enviadas en una transacción) y aún nos sobra la mayor parte del gas.

Conclusión

En la vida real puede que nunca implemente árboles de Merkle por su cuenta. Hay bibliotecas bien conocidas y auditadas que puede utilizar y, por lo general, es mejor no implementar criptográficos primitivos por su cuenta. Pero espero que ahora comprenda mejor las pruebas de Merkle y pueda decidir cuándo es mejor usarlas.

Tenga en cuenta que, si bien las pruebas de Merkle preservan la integridad, no preservan la disponibilidad. Saber que nadie puede adueñarse de sus activos es una pequeña consolación si el almacenamiento de datos decide desactivar el acceso y no puede construir un árbol de Merkle para acceder a estos. Por tanto, es mejor usar los árboles de Merkle con algún tipo de almacenamiento descentralizado, como IPFS.

Vea aquí más de mi trabajoopens in a new tab.

Última actualización de la página: 18 de diciembre de 2025

lopens in a new tab

qopens in a new tab

wopens in a new tab

+5

Ver colaboradores