Verifying smart contracts
Smart contracts are designed to be “trustless”, meaning users shouldn’t have to trust third parties (e.g., developers and companies) before interacting with a contract. As a requisite for trustlessness, users and other developers must be able to verify a smart contract’s source code. Source code verification assures users and developers that the published contract code is the same code running at the contract address on the Ethereum blockchain.
It is important to make the distinction between "source code verification" and "formal verification". Source code verification, which will be explained in detail below, refers to verifying that the given source code of a smart contract in a high-level language (e.g. Solidity) compiles to the same bytecode to be executed at the contract address. However, formal verification describes verifying the correctness of a smart contract, meaning the contract behaves as expected. Although context-dependent, contract verification usually refers to source code verification.
What is source code verification?
Before deploying a smart contract in the Ethereum Virtual Machine (EVM), developers compile the contract’s source code—instructions written in Solidity or another high-level programming language—to bytecode. As the EVM cannot interpret high-level instructions, compiling source code to bytecode (i.e., low-level, machine instructions) is necessary for executing contract logic in the EVM.
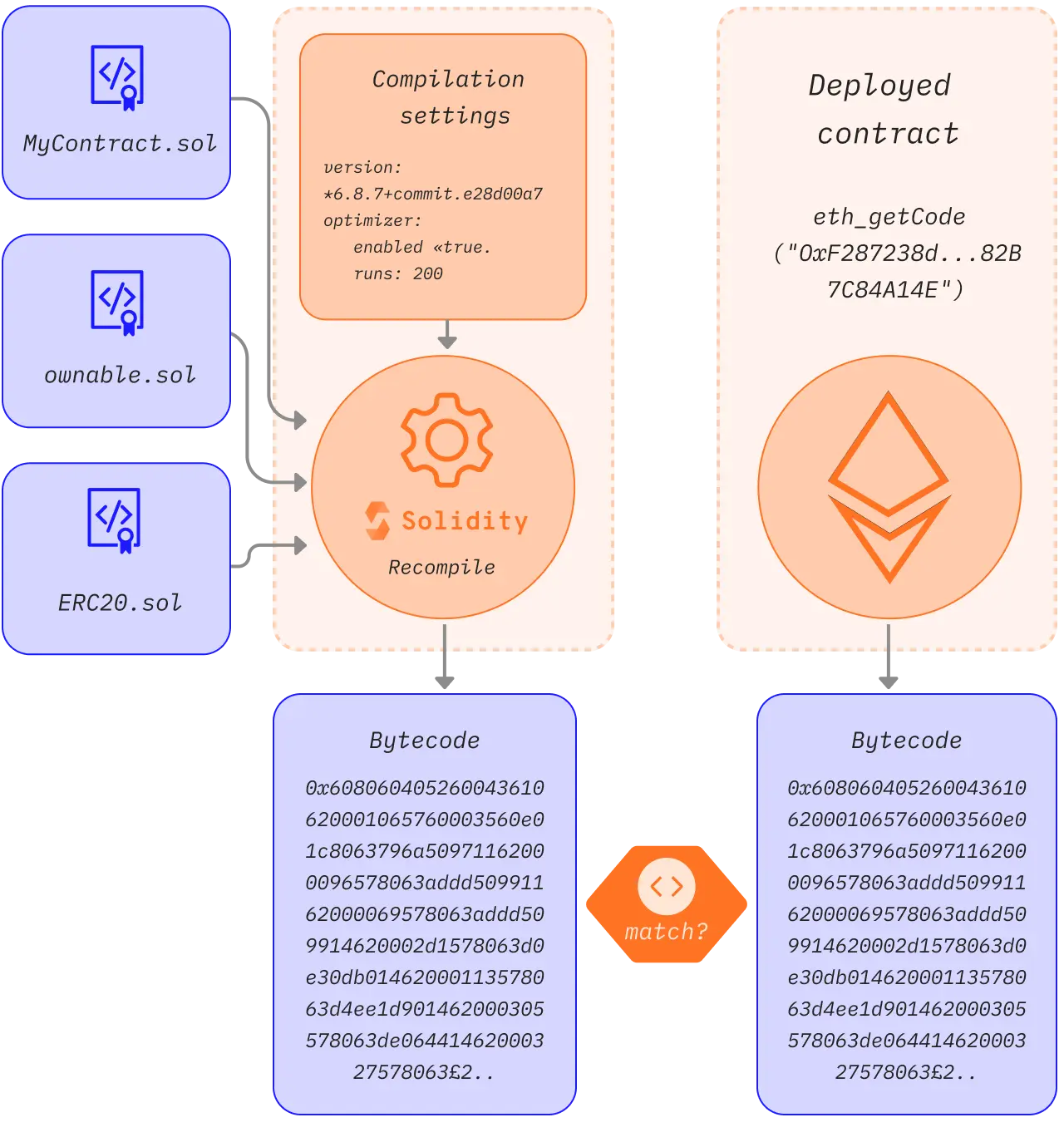
Source code verification is comparing a smart contract’s source code and the compiled bytecode used during the contract creation to detect any differences. Verifying smart contracts matters because the advertised contract code may be different from what runs on the blockchain.
Smart contract verification enables investigating what a contract does through the higher-level language it is written in, without having to read machine code. Functions, values, and usually the variable names and comments remain the same with the original source code that is compiled and deployed. This makes reading code much easier. Source verification also makes provision for code documentation, so that end-users know what a smart contract is designed to do.
What is full verification?
There are some parts of the source code that do not affect the compiled bytecode such as comments or variable names. That means two source codes with different variable names and different comments would both be able to verify the same contract. With that, a malicious actor can add deceiving comments or give misleading variable names inside the source code and get the contract verified with a source code different than the original source code.
It is possible to avoid this by appending extra data to the bytecode to serve as a cryptographic guarantee for the exactness of the source code, and as a fingerprint of the compilation information. The necessary information is found in the Solidity's contract metadata, and the hash of this file is appended to the bytecode of a contract. You can see it in action in the metadata playground
The metadata file contains information about the compilation of the contract including the source files and their hashes. Meaning, if any of the compilation settings or even a byte in one of the source files change, the metadata file changes. Consequently the hash of the metadata file, which is appended to the bytecode, also changes. That means if a contract's bytecode + the appended metadata hash match with the given source code and compilation settings, we can be sure this is exactly the same source code used in the original compilation, not even a single byte is different.
This type of verification that leverages the metadata hash is referred to as "full verification" (also "perfect verification"). If the metadata hashes do not match or are not considered in verification it would be a "partial match", which currently is the more common way to verify contracts. It is possible to insert malicious code that wouldn't be reflected in the verified source code without full verification. Most developers are not aware of the full verification and don't keep the metadata file of their compilation, hence partial verification has been the de facto method to verify contracts so far.
Why is source code verification important?
Trustlessness
Trustlessness is arguably the biggest premise for smart contracts and decentralized applications (dapps). Smart contracts are “immutable” and cannot be altered; a contract will only execute the business logic defined in the code at the time of deployment. This means developers and enterprises cannot tamper with a contract's code after deploying on Ethereum.
For a smart contract to be trustless, the contract code should be available for independent verification. While the compiled bytecode for every smart contract is publicly available on the blockchain, low-level language is difficult to understand—for both developers and users.
Projects reduce trust assumptions by publishing the source code of their contracts. But this leads to another problem: it is difficult to verify that the published source code matches the contract bytecode. In this scenario, the value of trustlessness is lost because users have to trust developers not to change a contract's business logic (i.e., by changing the bytecode) before deploying it on the blockchain.
Source code verification tools provide guarantees that a smart contract’s source code files matches the assembly code. The result is a trustless ecosystem, where users don’t blindly trust third parties and instead verify code before depositing funds into a contract.
User Safety
With smart contracts, there’s usually a lot of money at stake. This calls for higher security guarantees and verification of a smart contract’s logic before using it. The problem is that unscrupulous developers can deceive users by inserting malicious code in a smart contract. Without verification, malicious smart contracts can have backdoors, controversial access control mechanisms, exploitable vulnerabilities, and other things that jeopardize user safety that would go undetected.
Publishing a smart contract's source code files makes it easier for those interested, such as auditors, to assess the contract for potential attack vectors. With multiple parties independently verifying a smart contract, users have stronger guarantees of its security.
How to verify source code for Ethereum smart contracts
Deploying a smart contract on Ethereum requires sending a transaction with a data payload (compiled bytecode) to a special address. The data payload is generated by compiling the source code, plus the constructor arguments of the contract instance appended to the data payload in the transaction. Compilation is deterministic, meaning it always produces the same output (i.e., contract bytecode) if the same source files, and compilation settings (e.g. compiler version, optimizer) are used.
Verifying a smart contract basically involves the following steps:
-
Input the source files and compilation settings to a compiler.
-
Compiler outputs the bytecode of the contract
-
Get the bytecode of the deployed contract at a given address
-
Compare the deployed bytecode with the recompiled bytecode. If the codes match, the contract gets verified with the given source code and compilation settings.
-
Additionally, if the metadata hashes at the end of the bytecode match, it will be a full match.
Note that this is a simplistic description of verification and there are many exceptions that would not work with this such as having immutable variables.
Source code verification tools
The traditional process of verifying contracts can be complex. This is why we have tools for verifying source code for smart contracts deployed on Ethereum. These tools automate large parts of the source code verification and also curate verified contracts for the benefits of users.
Etherscan
Although mostly known as an Ethereum blockchain explorer, Etherscan also offers a source code verification service for smart contract developers and users.
Etherscan allows you to recompile contract bytecode from the original data payload (source code, library address, compiler settings, contract address, etc.) If the recompiled bytecode is associated with the bytecode (and constructor parameters) of the onchain contract, then the contract is verified.
Once verified, your contract’s source code receives a "Verified" label and is published on Etherscan for others to audit. It also gets added to the Verified Contracts section—a repository of smart contracts with verified source codes.
Etherscan is the most used tool for verifying contracts. However, Etherscan's contract verification has a drawback: it fails to compare the metadata hash of the onchain bytecode and recompiled bytecode. Therefore the matches in Etherscan are partial matches.
More on verifying contracts on Etherscan.
Sourcify
Sourcify is another tool for verifying contracts that is open-sourced and decentralized. It is not a block explorer and only verifies contracts on different EVM based networks. It acts as a public infrastructure for other tools to build on top of it, and aims to enable more human-friendly contract interactions using the ABI and NatSpec comments found in the metadata file.
Unlike Etherscan, Sourcify supports full matches with the metadata hash. The verified contracts are served in its public repository on HTTP and IPFS, which is a decentralized, content-addressed storage. This allows fetching the metadata file of a contract over IPFS since the appended metadata hash is an IPFS hash.
Additionally, one can also retrieve the source code files over IPFS, as IPFS hashes of these files are also found in the metadata. A contract can be verified by providing the metadata file and source files over its API or the UI, or using the plugins. Sourcify monitoring tool also listens to contract creations on new blocks and tries to verify the contracts if their metadata and source files are published on IPFS.
More on verifying contracts on Sourcify.
Tenderly
The Tenderly platform enables Web3 developers to build, test, monitor, and operate smart contracts. Combining debugging tools with observability and infrastructure building blocks, Tenderly helps developers accelerate smart contract development. To fully enable Tenderly features, developers need to perform source code verification using several methods.
It's possible to verify a contract privately or publicly. If verified privately, the smart contract is visible only to you (and other members in your project). Verifying a contract publicly makes it visible to everyone using the Tenderly platform.
You can verify your contracts using the Dashboard, Tenderly Hardhat plugin, or CLI.
When verifying contracts through the Dashboard, you need to import the source file or the metadata file generated by the Solidity compiler, the address/network, and compiler settings.
Using the Tenderly Hardhat plugin allows for more control over the verification process with less effort, enabling you to choose between automatic (no-code) and manual (code-based) verification.