离线数据完整性的默克尔证明
简介
理想的情况下,我们想要将所有东西存储在以太坊存储器中。这些数据存储于数以千计的计算机中 且有极高的可用性(数据不会被审查)和完整性(不能在未经授权的情况下修改数据), 但存储一个 32 字节的词一般需要花费 20,000 燃料。 在撰写此教程时,该费用 等于 6.60 美元。 每字节 21 美分对许多应用程序来说都过于昂贵。
为了解决这个问题,以太坊生态系统开发了许多以去中心化 方式存储数据的替代方法。 通常情况下, 需要在可用性与价格之间进行取舍。 然而,完整性通常可以得到保证。
在本文中,你将学习如何使用 默克尔证明 (opens in a new tab),在不将数据存储在区块链上的情况下确保数据完整性。
工作原理
理论上,我们只需将数据的哈希存储在链上,并在需要它的交易中发送所有数据。 但是,这会非常昂贵。 1 字节的数据通过交易发送的成本约 16 个燃料,目前约 0.5 美分,或每千字节约 5 美元。 每兆字节 5,000 美元,这对于许多应用程序来说仍然太昂贵,而且还没有加上对数据进行哈希计算的费用。
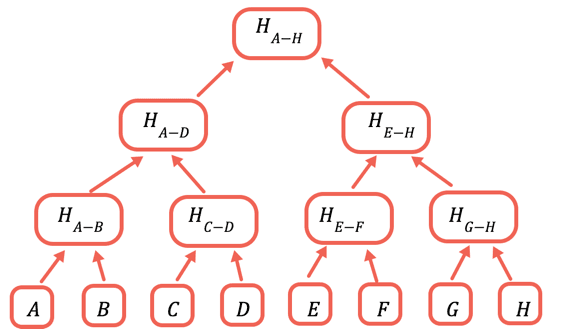
解决办法是反复对不同的数据子集进行哈希计算。对于不需要发送的数据,只要发送哈希值即可。 默克尔树是一种树型数据结构,每个节点值都是其下方节点的哈希值:
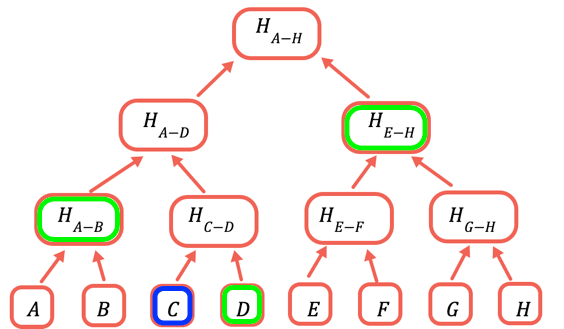
根哈希是唯一需要存储在链上的部分。 为了证明一个特定值,你需要提供所有与之合并才能获取根的哈希值。 例如,要证明 C,你需要提供 D、H(A-B) 和 H(E-H)。
实现
此处提供了示例代码 (opens in a new tab)。
链下代码
在本文中,我们使用 JavaScript 进行链下计算。 大多数去中心化应用程序的 JavaScript 中都有其链下组件。
创建默克尔根
首先,我们需要向区块链提供默克尔根。
1const ethers = require("ethers")我们使用 ethers 包中的哈希函数 (opens in a new tab)。
1// 需要我们验证其完整性的原始数据。前两个字节2// 是用户标识符,后两个字节是该3// 用户当前拥有的代币数量。4const dataArray = [5 0x0bad0010, 0x60a70020, 0xbeef0030, 0xdead0040, 0xca110050, 0x0e660060,6 0xface0070, 0xbad00080, 0x060d0091,7]例如,将每条数据编码为单个 256 位整数,并以非 JSON 的格式存储。 然而,这意味着在提取合约中的数据时,可以大大减少处理工作,从而显著降低了燃料成本。 你可以在链上读取 JSON (opens in a new tab),但如果可以避免,最好不要这么做。
1// 作为 BigInt 的哈希值数组2const hashArray = dataArray在此例中,我们的数据开始就是 256 位,因此不需要处理。 如果我们使用更复杂的数据结构,如字符串,我们需要确保先取数据的哈希值并获取哈希数组。 请注意,还有一个原因是我们不关心用户是否知道其他用户的信息。 否则,我们将不得不进行散列计算,使用户 1 不知道用户 0 的值,用户 2 不知道用户 3 的值,等等。
1// 在哈希函数所需的字符串与2// 我们在其他任何地方使用的 BigInt 之间进行转换。3const hash = (x) =>4 BigInt(ethers.utils.keccak256("0x" + x.toString(16).padStart(64, 0)))ethers 哈希函数需要一个包含十六进制数的 JavaScript 字符串(例如 0x60A7),并返回另一个具有相同结构的字符串。 但是,对于代码的其余部分,使用 BigInt 会更简单,因此我们将其转换为十六进制字符串,然后再转换回来。
1// 对称哈希一对值,这样我们就不必关心顺序是否颠倒。2const pairHash = (a, b) => hash(hash(a) ^ hash(b))这个函数是对称的(a xor (opens in a new tab) b 的哈希)。 这意味着在检查默克尔证明时,我们不必烦恼是将证明中的值放在计算值之前还是之后。 默克尔证明在链上进行检查,所以链上的操作越少越好。
警告:
密码学没有表面看起来那么容易。
本文的初始版本使用了哈希函数 hash(a^b)。
那是一个糟糕的想法,因为这意味着如果你知道 a 和 b 的合法值,就可以使用 b' = a^b^a' 来证明任何你想要的 a' 值。
使用这个函数,你必须计算 b',使得 hash(a') ^ hash(b') 等于一个已知值(通往根节点的下一个分支),这就困难得多了。
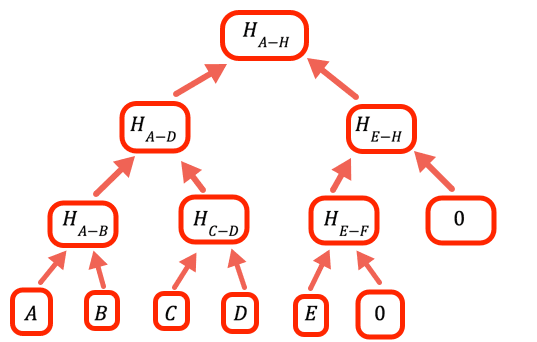
1// The value to denote that a certain branch is empty, doesn't2// have a value3const empty = 0n如果值的数量不是 2 的整数次方,我们需要处理空分支。 该程序的处理方式是将 0 作为占位符。
1// 通过按顺序获取每对值的哈希,2// 计算哈希数组在树中的上一层3const oneLevelUp = (inputArray) => {4 var result = []5 var inp = [...inputArray] // 避免覆盖输入 // 如有必要,添加一个空值(我们需要所有的叶子都 // 配对)67 if (inp.length % 2 === 1) inp.push(empty)89 for (var i = 0; i < inp.length; i += 2)10 result.push(pairHash(inp[i], inp[i + 1]))1112 return result13} // oneLevelUp显示全部此函数通过对默克尔树中当前层级的值对进行哈希处理来上升一个层级。 请注意,这不是最高效的实现,我们本可以避免复制输入,只需在循环中的适当位置添加 hashEmpty,但此代码为可读性进行了优化。
1const getMerkleRoot = (inputArray) => {2 var result34 result = [...inputArray] // 沿树向上,直到只剩一个值,这个值就是 // 根。 // // 如果某一层有奇数个条目, // oneLevelUp 中的代码会添加一个空值,因此如果我们有(例如) // 10 个叶子,那么第二层将有 5 个分支,第三层 // 有 3 个,第四层有 2 个,根是第五个56 while (result.length > 1) result = oneLevelUp(result)78 return result[0]9}显示全部要到达根,一直上升到只剩下一个值的层级。
创建默克尔证明
默克尔证明是与要证明的值一起哈希处理以便返回默克尔根的值。 要证明的值往往来自其他数据,因此这里更愿意单独提供,而不是作为代码的一部分。
1// 默克尔证明包含与之哈希的条目2// 列表的值。因为我们使用了对称哈希函数,我们不3// 需要条目的位置来验证证明,只需要用它来创建证明4const getMerkleProof = (inputArray, n) => {5 var result = [], currentLayer = [...inputArray], currentN = n67 // 直到我们到达顶部8 while (currentLayer.length > 1) {9 // 没有奇数长度的层10 if (currentLayer.length % 2)11 currentLayer.push(empty)1213 result.push(currentN % 214 // 如果 currentN 是奇数,则将其之前的值添加到证明中15 ? currentLayer[currentN-1]16 // 如果是偶数,则添加其后的值17 : currentLayer[currentN+1])18显示全部我们对 (v[0],v[1])、(v[2],v[3]) 等进行哈希。 因此,对于偶数值,我们需要下一个值,而奇数值则需要上一个值。
1 // 移动到上一层2 currentN = Math.floor(currentN/2)3 currentLayer = oneLevelUp(currentLayer)4 } // while currentLayer.length > 156 return result7} // getMerkleProof链上代码
最后,我们有核查证明的代码。 链上代码是用 Solidity (opens in a new tab) 编写的。 优化在这里更为重要,因为燃料费相对昂贵。
1//SPDX-License-Identifier: Public Domain2pragma solidity ^0.8.0;34import "hardhat/console.sol";编写此代码时,我使用的是安全帽开发环境 (opens in a new tab),它使我们在开发过程中可以获得 Solidity 的控制台输出 (opens in a new tab)。
12contract MerkleProof {3 uint merkleRoot;45 function getRoot() public view returns (uint) {6 return merkleRoot;7 }89 // 极不安全,在生产代码中,对10 // 此函数的访问权限必须受到严格限制,可能仅限于11 // 所有者12 function setRoot(uint _merkleRoot) external {13 merkleRoot = _merkleRoot;14 } // setRoot显示全部为默克尔根设置和获取函数。 在生产系统中,允许任何人更新默克尔根是一个_极其糟糕的主意_。 这里这样做是为了简化示例代码。 不要在数据完整性至关重要的系统上这样做。
1 function hash(uint _a) internal pure returns(uint) {2 return uint(keccak256(abi.encode(_a)));3 }45 function pairHash(uint _a, uint _b) internal pure returns(uint) {6 return hash(hash(_a) ^ hash(_b));7 }此函数生成一个配对哈希值。 这只是 hash 和 pairHash 的 JavaScript 代码的 Solidity 翻译版本。
**注意:**这是另一个为可读性而优化的例子。 根据函数定义 (opens in a new tab),或许可以将数据存储为 bytes32 (opens in a new tab) 值,从而避免转换。
1 // 验证默克尔证明2 function verifyProof(uint _value, uint[] calldata _proof)3 public view returns (bool) {4 uint temp = _value;5 uint i;67 for(i=0; i<_proof.length; i++) {8 temp = pairHash(temp, _proof[i]);9 }1011 return temp == merkleRoot;12 }1314} // MarkleProof显示全部用数学符号表示,默克尔证明验证如下所示:H(proof_n, H(proof_n-1, H(proof_n-2, ... H(proof_1, H(proof_0, value))...)))`。 此代码实现了默克尔证明。
默克尔证明与卷叠
默克尔证明不能与卷叠很好地配合使用。 原因在于,卷叠将所有交易数据写入一层网络,但在二层网络进行处理。 发送交易的默克尔证明的成本平均达到每个层级 638 个燃料(目前,如果字节不为零,调用数据中一个字节花费 16 个燃料,如果为零,则花费 4 个燃料)。 如果我们的数据包含 1024 个字,默克尔证明需要 10 个层级,或者总共 6380 个燃料。
以 Optimism (opens in a new tab) 为例,写入 L1 的燃料成本约为 100 gwei,写入 L2 的燃料成本为 0.001 gwei(这是正常价格,拥堵时可能会上涨)。 所以对于一层网络上 1 个燃料的成本,我们可能需要在二层网络上花费 10 万个燃料的处理费用。 假定我们不用重写存储,这意味着我们可以用一个一层网络燃料的价格将大约五个字写入二层网络的存储中。 对于单个默克尔证明,我们可以将全部 1024 个字写入存储(假设它们一开始就可以在链上计算,而不是在交易中提供),并且仍然有大部分燃料剩余。
结论
在现实中,你可能永远不会独立实现默克尔树。 有很多广为人知并经过审核的程序库可供使用,一般来说,最好不要自己独立实现加密基元。 但我希望你们现在能够更好地理解默克尔证明,并能够决定何时值得使用。
请注意,虽然默克尔证明可以保持_完整性_,但不能保持_可用性_。 如果数据存储方决定禁止访问,而且你不能构建默克尔树来访问你的资产,那么知道没有人可以拿走你的资产也只能作为一种小小的慰藉而已。 所以默克尔树最好和某种去中心化存储一起使用,例如星际文件系统。
点击此处查看我的更多作品 (opens in a new tab)。
页面最后更新: 2025年12月18日