Preuves de Merkle relatives à l'intégrité des données hors ligne

Introduction

Idéalement, nous souhaiterions tout conserver dans le stockage Ethereum, qui est lui-même stocké sur des milliers d'ordinateurs et bénéficie ainsi d'une disponibilité extrêmement élevée (les données ne peuvent pas être censurées) et d'une grande intégrité (les données ne peuvent pas être modifiées de manière non autorisée) sachant, cependant, que stocker un mot de 32 octets coûte normalement 20 000 gaz. Ce que je vais écrire ici aurait un coût équivalent à 6,60 $. À 21 cents par octet, c'est trop cher pour beaucoup d'utilisations.

Pour résoudre ce problème, l'écosystème Ethereum a développé de nombreuses façons alternatives de stocker des données de manière décentralisée. Habituellement, elles impliquent un compromis entre disponibilité et prix. Toutefois, l’intégrité est généralement assurée.

Dans cet article, vous apprendrez comment garantir l'intégrité des données sans les stocker sur la blockchain, en utilisant les preuves de Merkle (opens in a new tab).

Comment ça marche ?

En théorie, nous pourrions simplement stocker le hachage des données en chaîne, et envoyer toutes les données dans les transactions qui le requièrent. Cependant, cela reste encore trop cher. Un octet de données lors d'une transaction a un coût d'environ 16 gaz, soit environ un demi-cent actuellement ou environ 5 $ par kilo-octets. À 5 000 $ le mégaoctet, c'est encore trop cher pour de nombreuses utilisations même sans le coût supplémentaire de hachage des données.

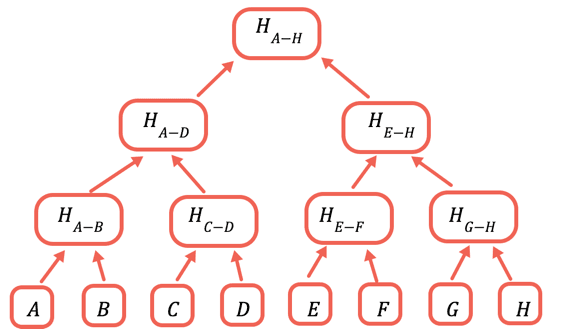
La solution est de hacher de façon répétée différents sous-ensembles de données. Pour les données que vous n'avez pas besoin d'envoyer, vous pouvez ainsi juste envoyer un hachage. Vous pouvez le faire en utilisant un arbre de Merkle, une structure de données en arborescence où chaque nœud est un hachage des nœuds en dessous :

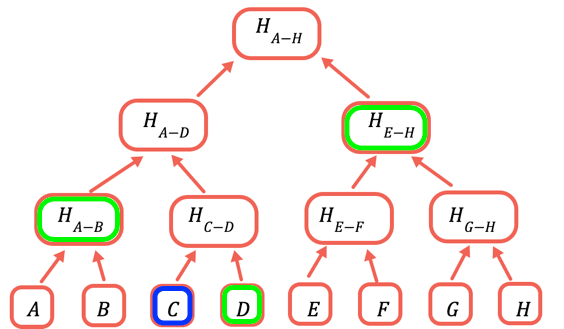
Le hachage racine est la seule partie qui doit être stockée en chaîne. Pour prouver une certaine valeur, vous fournissez tous les hachages qui doivent être combinés avec elle pour obtenir la racine. Par exemple, pour prouver C, vous fournissez D, H(A-B) et H(E-H).

Implémentation

L'exemple de code est fourni ici (opens in a new tab).

Code hors chaîne

Dans cet article, nous utilisons JavaScript pour les calculs hors chaîne. La plupart des applications décentralisées ont leur composant hors chaîne en JavaScript.

Création de la racine de Merkle

Premièrement, nous devons apporter la racine Merkle à la chaîne.

1const ethers = require("ethers")

Nous utilisons la fonction de hachage du package ethers (opens in a new tab).

1// Les données brutes dont nous devons vérifier l'intégrité. Les deux premiers octets
2// sont un identifiant d'utilisateur, et les deux derniers octets le montant de jetons que
3// l'utilisateur possède actuellement.
4const dataArray = [
5  0x0bad0010, 0x60a70020, 0xbeef0030, 0xdead0040, 0xca110050, 0x0e660060,
6  0xface0070, 0xbad00080, 0x060d0091,
7]

Encoder chaque entrée sur un seul entier de 256 bits donne un code moins lisible que JSON, par exemple. Cependant, cela signifie un traitement beaucoup moins important pour récupérer les données contenues dans le contrat et ainsi, des frais de gaz moins élevés. Vous pouvez lire du JSON en chaîne (opens in a new tab), mais c'est une mauvaise idée si c'est évitable.

1// The array of hash values, as BigInts
2const hashArray = dataArray

Dans notre cas et pour commencer, nos données ont une valeur de 256 bits. Ainsi, aucun traitement n'est nécessaire. Si nous utilisons une structure de données plus compliquée, comme des chaînes de caractères, nous devons nous assurer de d'abord hacher les données pour obtenir un tableau de hachages. Notez que c'est aussi parce que nous ne nous soucions pas de savoir que les utilisateurs connaissent les informations des autres utilisateurs. Sinon, nous aurions dû réaliser un hachage de sorte que l'utilisateur 1 ne connaisse pas la valeur pour l'utilisateur 0, que l'utilisateur 2 ne connaisse pas la valeur pour l'utilisateur 3, etc.

1// Convertit entre la chaîne de caractères attendue par la fonction de hachage et le
2// BigInt que nous utilisons partout ailleurs.
3const hash = (x) =>
4  BigInt(ethers.utils.keccak256("0x" + x.toString(16).padStart(64, 0)))

La fonction de hachage d'ethers s'attend à recevoir une chaîne de caractères JavaScript avec un nombre hexadécimal, tel que 0x60A7, et répond avec une autre chaîne de caractères de même structure. Cependant, pour le reste du code, il est plus facile d'utiliser BigInt, nous convertissons donc en une chaîne hexadécimale et vice-versa.

1// Hachage symétrique d'une paire pour que l'inversion de l'ordre n'ait pas d'importance.
2const pairHash = (a, b) => hash(hash(a) ^ hash(b))

Cette fonction est symétrique (hachage de a xor (opens in a new tab) b). Cela signifie que lorsque nous vérifions la preuve de Merkle, nous n'avons pas à nous soucier de savoir s'il faut mettre la valeur de la preuve avant ou après la valeur calculée. La vérification des preuves de Merkle se fait en chaîne, donc moins nous avons d'opérations à y effectuer, mieux c'est.

Attention : La cryptographie est plus complexe qu'il n'y paraît. La version initiale de cet article avait la fonction de hachage hash(a^b). C'était une mauvaise idée car cela signifiait que si vous connaissiez les valeurs légitimes de a et b, vous pouviez utiliser b' = a^b^a' pour prouver n'importe quelle valeur a' désirée. Avec cette fonction, vous devriez calculer b' de telle sorte que hash(a') ^ hash(b') soit égal à une valeur connue (la branche suivante sur le chemin de la racine), ce qui est beaucoup plus difficile.

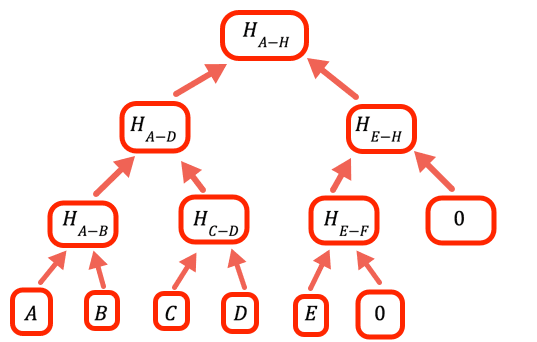
1// The value to denote that a certain branch is empty, doesn't
2// have a value
3const empty = 0n

Lorsque le nombre de valeurs n'est pas un nombre entier à deux chiffres, nous devons gérer les branches vides. Pour ce faire, le programme va mettre un zéro à la place.

1// Calcule un niveau supérieur de l'arbre d'un tableau de hachage en prenant le hachage de
2// chaque paire en séquence
3const oneLevelUp = (inputArray) => {
4  var result = []
5  var inp = [...inputArray] // Pour éviter d'écraser l'entrée // Ajoute une valeur vide si nécessaire (nous avons besoin que toutes les feuilles soient // appariées)
6
7  if (inp.length % 2 === 1) inp.push(empty)
8
9  for (var i = 0; i < inp.length; i += 2)
10    result.push(pairHash(inp[i], inp[i + 1]))
11
12  return result
13} // oneLevelUp
Afficher tout

Cette fonction « escalade » un niveau dans l'arbre de Merkle en hachant les paires de valeurs de la couche actuelle. Notez que ce n'est pas l'implémentation la plus efficace, nous aurions pu éviter de copier l'entrée et juste ajouter hashEmpty lorsque cela est approprié dans la boucle, mais ce code est optimisé pour la lisibilité.

1const getMerkleRoot = (inputArray) => {
2  var result
3
4  result = [...inputArray] // Remonte l'arbre jusqu'à ce qu'il n'y ait plus qu'une seule valeur, qui est la // racine. // // Si une couche a un nombre impair d'entrées, le // code dans oneLevelUp ajoute une valeur vide, donc si nous avons, par exemple, // 10 feuilles, nous aurons 5 branches dans la deuxième couche, 3 // branches dans la troisième, 2 dans la quatrième et la racine est la cinquième
5
6  while (result.length > 1) result = oneLevelUp(result)
7
8  return result[0]
9}
Afficher tout

Pour obtenir la racine, escaladez jusqu'à ce qu'il ne reste qu'une seule valeur.

Création d'une preuve de Merkle

Une preuve de Merkle est l'ensemble des valeurs à hacher ensemble avec la valeur prouvée pour récupérer la racine de Merkle. La valeur à prouver est souvent disponible à partir d'autres données. Je préfère ainsi la fournir séparément plutôt que dans le cadre du code.

1// Une preuve de Merkle consiste en la valeur de la liste des entrées à
2// hacher. Comme nous utilisons une fonction de hachage symétrique, nous n'avons pas
3// besoin de l'emplacement de l'élément pour vérifier la preuve, seulement pour la créer
4const getMerkleProof = (inputArray, n) => {
5    var result = [], currentLayer = [...inputArray], currentN = n
6
7    // Jusqu'à ce que nous atteignons le sommet
8    while (currentLayer.length > 1) {
9        // Pas de couches de longueur impaire
10        if (currentLayer.length % 2)
11            currentLayer.push(empty)
12
13        result.push(currentN % 2
14               // Si currentN est impair, l'ajouter à la preuve avec la valeur qui le précède
15            ? currentLayer[currentN-1]
16               // S'il est pair, ajouter la valeur qui le suit
17            : currentLayer[currentN+1])
18
Afficher tout

Nous hachons (v[0],v[1]), (v[2],v[3]), etc. Ainsi, pour les valeurs uniques, nous avons besoin de la suivante, pour les valeurs impaires de la précédente.

1        // Passer à la couche supérieure
2        currentN = Math.floor(currentN/2)
3        currentLayer = oneLevelUp(currentLayer)
4    }   // tant que currentLayer.length > 1
5
6    return result
7}   // getMerkleProof

Code en chaîne

Enfin, nous avons le code qui vérifie la preuve. Le code en chaîne est écrit en Solidity (opens in a new tab). L'optimisation est beaucoup plus importante ici parce que les frais en gaz sont relativement élevés.

1//SPDX-License-Identifier: Public Domain
2pragma solidity ^0.8.0;
3
4import "hardhat/console.sol";
Copier

J'ai écrit ceci en utilisant l'environnement de développement Hardhat (opens in a new tab), qui nous permet d'avoir une sortie de console depuis Solidity (opens in a new tab) pendant le développement.

1
2contract MerkleProof {
3    uint merkleRoot;
4
5    function getRoot() public view returns (uint) {
6      return merkleRoot;
7    }
8
9    // Extrêmement peu sûr, dans le code de production, l'accès à
10    // cette fonction DOIT ÊTRE strictement limité, probablement à un
11    // propriétaire
12    function setRoot(uint _merkleRoot) external {
13      merkleRoot = _merkleRoot;
14    }   // setRoot
Afficher tout
Copier

Définissez et obtenez des fonctions pour la racine de Merkle. Laisser tout le monde mettre à jour la racine de Merkle est une très mauvaise idée dans un système de production. Je le fais ici par souci de simplicité pour l'exemple de code. Ne le faites pas sur un système où l'intégrité des données importe réellement.

1    function hash(uint _a) internal pure returns(uint) {
2      return uint(keccak256(abi.encode(_a)));
3    }
4
5    function pairHash(uint _a, uint _b) internal pure returns(uint) {
6      return hash(hash(_a) ^ hash(_b));
7    }
Copier

Cette fonction génère un hachage de la paire. Il s'agit simplement de la traduction en Solidity du code JavaScript pour hash et pairHash.

Remarque : C'est un autre cas d'optimisation pour la lisibilité. D'après la définition de la fonction (opens in a new tab), il pourrait être possible de stocker les données sous la forme d'une valeur bytes32 (opens in a new tab) et d'éviter les conversions.

1    // Vérifier une preuve de Merkle
2    function verifyProof(uint _value, uint[] calldata _proof)
3        public view returns (bool) {
4      uint temp = _value;
5      uint i;
6
7      for(i=0; i<_proof.length; i++) {
8        temp = pairHash(temp, _proof[i]);
9      }
10
11      return temp == merkleRoot;
12    }
13
14}  // MerkleProof
Afficher tout
Copier

En notation mathématique, la vérification de la preuve de Merkle ressemble à ceci : H(proof_n, H(proof_n-1, H(proof_n-2, ... H(proof_1, H(proof_0, value))...))). Ce code l'implémente.

Les preuves de Merkle et les rollups ne font pas bon ménage

Les preuves de Merkle ne fonctionnent pas bien avec les rollups. La raison en est que les rollups écrivent toutes les données de transaction sur L1, mais le processus sur L2. Le coût d'envoi d'une preuve Merkle avec une transaction est en moyenne de 638 gaz par couche (actuellement, un octet de données d'appel coûte 16 gaz s'il n'est pas nul, et 4 s'il est nul). Si nous avons 1 024 mots de données, une preuve de Merkle nécessite dix couches, soit un total de 6 380 gaz.

Si l'on prend l'exemple d'Optimism (opens in a new tab), l'écriture du gaz L1 coûte environ 100 gwei et le gaz L2 coûte 0,001 gwei (c'est le prix normal, il peut augmenter en cas de congestion). Ainsi, pour le coût d'un gaz L1, nous pouvons dépenser cent mille gaz pour le traitement L2. En supposant que nous n'ayons pas écrasé le stockage, cela signifie que nous pouvons écrire environ cinq mots à stocker sur L2 pour le prix d'un gaz L1. Pour une seule preuve de Merkle, nous pouvons écrire les 1024 mots entiers dans le stockage (en supposant qu'ils peuvent être calculés en chaîne pour commencer, plutôt que fournis dans une transaction) et il nous restera toujours la plus grande partie du gaz.

Conclusion

Dans la vie réelle, il se peut que vous n'ayez jamais à implémenter d'arbres de Merkle par vous-même. Il existe des bibliothèques bien connues et auditées que vous pouvez utiliser et, en général, il est préférable de ne pas implémenter des primitives cryptographiques par vous-même. Cependant, j'espère que, maintenant, vous comprendrez mieux les preuves de Merkle et que vous pourrez décider quand elles valent la peine d'être utilisées.

Notez que si les preuves de Merkle préservent l'intégrité, elles ne préservent pas la disponibilité. Savoir que personne d'autre ne peut se saisir de vos actifs est une petite consolation si le stockage de données décide d'en interdire l'accès et que vous ne pouvez pas non plus construire un arbre de Merkle pour y accéder. Ainsi, les arbres de Merkle sont mieux utilisés avec un type de stockage décentralisé, comme IPFS.

Voir ici pour plus de mon travail (opens in a new tab).

Dernière mise à jour de la page : 18 décembre 2025

l (opens in a new tab)

q (opens in a new tab)

w (opens in a new tab)

+5

Voir les contributeurs