Provas de Merkle para integridade de dados offline

armazenamento

Avançado

Ori Pomerantz

30 de dezembro de 2021

11 minutos de leitura

Introdução

Idealmente, gostaríamos de guardar tudo no armazenamento do Ethereum, que é armazenado em milhares de computadores e conta com uma disponibilidade extremamente alta (os dados não podem ser censurados) e integridade (os dados não podem ser modificados de forma não autorizada), sabendo que armazenar uma palavra de 32 bytes normalmente custa 20.000 gás. No momento em que estou escrevendo isto, o custo é equivalente a $6,60. A 21 centavos por byte, isso é bastante caro para muitas utilizações.

Para resolver esse problema, o ecossistema da Ethereum desenvolveu muitas maneiras alternativas de armazenar dados de forma descentralizada. Geralmente, elas envolvem um equilíbrio entre a disponibilidade e o preço. No entanto, a integridade é geralmente assegurada.

Neste artigo, você aprenderá como garantir a integridade dos dados sem armazenar os dados na blockchain, usando provas de Merkle (opens in a new tab).

Como isso funciona?

Em teoria, poderíamos apenas armazenar o hash dos dados na cadeia e enviar todos os dados em transações que o exigem. No entanto, isso ainda é demasiado caro. Um byte de dados para uma transação custa cerca de 16 gás, atualmente cerca de meio centavo ou cerca de $5 por kilobyte. A $5.000 por megabyte, isso ainda é muito caro para várias utilizações, mesmo sem o custo adicional de hashing de dados.

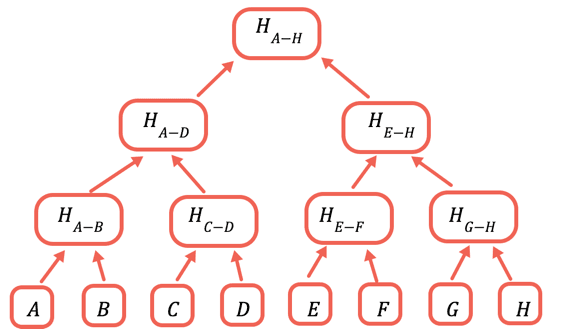
A solução é fazer hash repetidamente de diferentes subconjuntos dos dados. Para os dados que você não precisa enviar, você pode apenas enviar um hash. Você pode fazer isso usando uma árvore de Merkle, uma estrutura de dados de árvore em que cada nó é um hash dos nós abaixo:

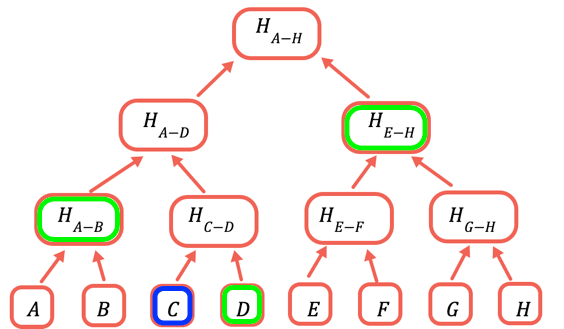
O hash raiz é a única parte que precisa ser armazenada na cadeia. Para comprovar um determinado valor, forneça todos os hashes que precisam ser combinados com ele para obter a raiz. Por exemplo, para provar C, você fornece D, H(A-B) e H(E-H).

Implementação

O código de exemplo é fornecido aqui (opens in a new tab).

Código fora da cadeia

Neste artigo, usamos JavaScript para os cálculos fora da cadeia. A maioria dos aplicativos descentralizados tem seu componente fora da cadeia em JavaScript.

Criando a raiz de Merkle

Primeiro, precisamos fornecer a raiz Merkle à cadeia.

1const ethers = require("ethers")

Usamos a função de hash do pacote ethers (opens in a new tab).

1// Os dados brutos cuja integridade temos que verificar. Os primeiros dois bytes a
2// são um identificador de usuário, e os dois últimos bytes a quantidade de tokens que o
3// usuário possui no momento.
4const dataArray = [
5  0x0bad0010, 0x60a70020, 0xbeef0030, 0xdead0040, 0xca110050, 0x0e660060,
6  0xface0070, 0xbad00080, 0x060d0091,
7]

Codificar cada entrada em um único inteiro de 256 bits resulta em um código menos legível que o JSON, por exemplo. No entanto, isso significa um processamento significativamente menor para recuperar os dados contidos no contrato, portanto, custos de gás muito menores. Você pode ler JSON na cadeia (opens in a new tab), mas é uma má ideia se for evitável.

1// A matriz de valores de hash, como BigInts
2const hashArray = dataArray

Nesse caso, para começar, nossos dados têm um valor 256 bits. Portanto, não é necessário qualquer tipo de processamento. Se usarmos uma estrutura de dados mais complicada, como cadeias de caracteres, precisamos ter certeza de que fazemos primeiro o hash dos dados para obter uma matriz de hashes. Observe que isso também é devido ao fato de não nos importarmos se usuários conhecem as informações de outros usuários. Caso contrário, teríamos tido que fazer um hash, para que o usuário 1 não saiba o valor para o usuário 0, ao usuário 2 que não saberá o valor para o usuário 3, etc.

1// Converte entre a string que a função de hash espera e o
2// BigInt que usamos em todos os outros lugares.
3const hash = (x) =>
4  BigInt(ethers.utils.keccak256("0x" + x.toString(16).padStart(64, 0)))

A função de hash ethers espera obter uma string JavaScript com um número hexadecimal, como 0x60A7, e responde com outra string com a mesma estrutura. No entanto, para o resto do código, é mais fácil usar BigInt, então convertemos para uma string hexadecimal e de volta novamente.

1// Hash simétrico de um par para que não nos importemos se a ordem for invertida.
2const pairHash = (a, b) => hash(hash(a) ^ hash(b))

Esta função é simétrica (hash de um xor (opens in a new tab) b). Isto significa que quando verificamos a prova de Merkle, não precisamos nos preocupar se devemos colocar o valor da prova antes ou depois do valor calculado. A verificação da prova de Merkle é feita na cadeia, portanto, quanto menos precisarmos fazer lá, melhor.

Atenção: A criptografia é mais difícil do que parece. A versão inicial deste artigo tinha a função de hash hash(a^b). Essa foi uma má ideia, porque significava que se você conhecesse os valores legítimos de a e b, você poderia usar b' = a^b^a' para provar qualquer valor a' desejado. Com esta função, você teria que calcular b' de tal forma que hash(a') ^ hash(b') seja igual a um valor conhecido (o próximo ramo a caminho da raiz), o que é muito mais difícil.

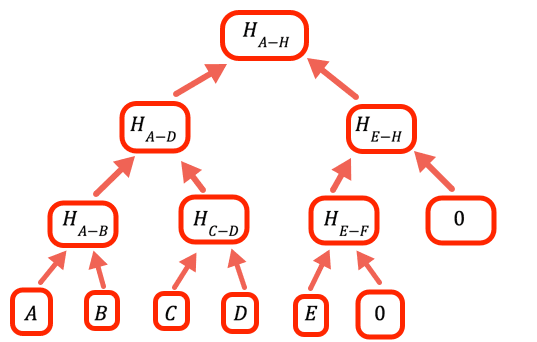
1// O valor para denotar que um determinado ramo está vazio, não
2// tem um valor
3const empty = 0n

Quando o número de valores não é uma potência inteira de dois, precisamos lidar com branches vazios. O programa faz isso colocando zero como espaço reservado.

1// Calcula um nível acima na árvore de uma matriz de hash, obtendo o hash de
2// cada par em sequência
3const oneLevelUp = (inputArray) => {
4  var result = []
5  var inp = [...inputArray] // Para evitar sobrescrever a entrada // Adicione um valor vazio se necessário (precisamos que todas as folhas sejam // pareadas)
6
7  if (inp.length % 2 === 1) inp.push(empty)
8
9  for (var i = 0; i < inp.length; i += 2)
10    result.push(pairHash(inp[i], inp[i + 1]))
11
12  return result
13} // oneLevelUp
Exibir tudo

Esta função “escala” um nível na árvore de Merkle, fazendo hash dos pares de valores na camada atual. Observe que esta não é a implementação mais eficiente, poderíamos ter evitado copiar a entrada e apenas adicionado hashEmpty quando apropriado no loop, mas este código é otimizado para legibilidade.

1const getMerkleRoot = (inputArray) => {
2  var result
3
4  result = [...inputArray] // Sobe na árvore até que haja apenas um valor, que é a // raiz. // // Se uma camada tem um número ímpar de entradas, o // código em oneLevelUp adiciona um valor vazio, então se tivermos, por exemplo, // 10 folhas, teremos 5 ramos na segunda camada, 3 // ramos na terceira, 2 na quarta e a raiz é a quinta
5
6  while (result.length > 1) result = oneLevelUp(result)
7
8  return result[0]
9}
Exibir tudo

Para obter a raiz, suba até que haja apenas um valor restante.

Criando uma prova de Merkle

Uma prova de Merkle é o conjunto de valores a fazer hash junto com o valor que está sendo provado para recuperar a raiz de Merkle. O valor a provar está frequentemente disponível a partir de outros dados, então eu prefiro fornecê-lo separadamente do que como parte do código.

1// Uma prova de merkle consiste no valor da lista de entradas para
2// fazer o hash. Como usamos uma função de hash simétrica, não
3// precisamos da localização do item para verificar a prova, apenas para criá-la
4const getMerkleProof = (inputArray, n) => {
5    var result = [], currentLayer = [...inputArray], currentN = n
6
7    // Até chegarmos ao topo
8    while (currentLayer.length > 1) {
9        // Nenhuma camada de comprimento ímpar
10        if (currentLayer.length % 2)
11            currentLayer.push(empty)
12
13        result.push(currentN % 2
14               // Se currentN for ímpar, adicione o valor anterior a ele à prova
15            ? currentLayer[currentN-1]
16               // Se for par, adicione o valor depois dele
17            : currentLayer[currentN+1])
18
Exibir tudo

Fazemos o hash de (v[0],v[1]), (v[2],v[3]), etc. Portanto, para valores pares, precisamos do próximo e, para valores ímpares, precisamos do anterior.

1        // Move para a próxima camada acima
2        currentN = Math.floor(currentN/2)
3        currentLayer = oneLevelUp(currentLayer)
4    }   // enquanto currentLayer.length > 1
5
6    return result
7}   // getMerkleProof

Código na cadeia

Por fim, temos o código que verifica a prova. O código na cadeia é escrito em Solidity (opens in a new tab). A otimização é aqui muito mais importante, porque o gás é relativamente caro.

1//SPDX-License-Identifier: Public Domain
2pragma solidity ^0.8.0;
3
4import "hardhat/console.sol";

Escrevi isso usando o ambiente de desenvolvimento Hardhat (opens in a new tab), que nos permite ter uma saída de console do Solidity (opens in a new tab) durante o desenvolvimento.

1
2contract MerkleProof {
3    uint merkleRoot;
4
5    function getRoot() public view returns (uint) {
6      return merkleRoot;
7    }
8
9    // Extremamente inseguro, em código de produção, o acesso a
10    // esta função DEVE SER estritamente limitado, provavelmente a um
11    // proprietário
12    function setRoot(uint _merkleRoot) external {
13      merkleRoot = _merkleRoot;
14    }   // setRoot
Exibir tudo

Configure e obtenha funções para a raiz de Merkle. Permitir que todos atualizem a raiz de Merkle é uma péssima ideia em um sistema de produção. Aqui, faço isso por uma questão de simplicidade no código de exemplo. Não faça isso em um sistema onde a integridade dos dados realmente importa.

1    function hash(uint _a) internal pure returns(uint) {
2      return uint(keccak256(abi.encode(_a)));
3    }
4
5    function pairHash(uint _a, uint _b) internal pure returns(uint) {
6      return hash(hash(_a) ^ hash(_b));
7    }

Essa função gera um par de hashes. É apenas a tradução em Solidity do código JavaScript para hash e pairHash.

Observação: este é outro caso de otimização para legibilidade. Com base na definição da função (opens in a new tab), pode ser possível armazenar os dados como um valor bytes32 (opens in a new tab) e evitar as conversões.

1    // Verifica uma prova de Merkle
2    function verifyProof(uint _value, uint[] calldata _proof)
3        public view returns (bool) {
4      uint temp = _value;
5      uint i;
6
7      for(i=0; i<_proof.length; i++) {
8        temp = pairHash(temp, _proof[i]);
9      }
10
11      return temp == merkleRoot;
12    }
13
14}  // MarkleProof
Exibir tudo

Em notação matemática, a verificação da prova de Merkle se parece com isto: H(proof_n, H(proof_n-1, H(proof_n-2, ... H(proof_1, H(proof_0, value))...))). Este código implementa-o.

Provas de Merkle e rollups não combinam

As provas de Merkle não funcionam bem com rollups. O motivo é que os rollups escrevem todos os dados da transação no L1, mas são processadas no L2. O custo para enviar uma prova de Merkle com uma média de transação a 638 gás por camada (atualmente, um byte nos dados de chamadas custa 16 gás se não for zero, e 4 se for zero). Se temos 1024 palavras de dados, uma prova de Merkle requer dez camadas, ou um total de 6380 gás.

Olhando, por exemplo, para o Optimism (opens in a new tab), escrever na L1 custa cerca de 100 gwei de gás e na L2 custa 0,001 gwei de gás (este é o preço normal, pode aumentar com o congestionamento). Portanto, pelo custo de um gás L1 podemos gastar cem mil gás no processamento L2. Supondo que não sobrescrevamos o armazenamento, isso significa que podemos escrever cerca de cinco palavras para armazenamento na L2 pelo preço de um gás L1. Para uma única prova de Merkle, podemos escrever todas as 1024 palavras no armazenamento (supondo que elas possam ser calculadas na cadeia para começar, em vez de serem fornecidas em uma transação) e ainda ter a maior parte do gás restante.

Conclusão

Na vida real, você pode nunca implementar Merkle por conta própria. Existem bibliotecas conhecidas e auditadas que você pode usar e, de um modo geral, é melhor não implementar primitivos criptográficos por conta própria. Mas espero que agora você compreenda melhor as provas de Merkle e que possa decidir quando é que vale a pena utilizar.

Observe que, embora as provas de Merkle preservem a integridade, elas não preservam a disponibilidade. Saber que mais ninguém pode tomar seus ativos é uma pequena consolação se o armazenamento de dados decidir impedir o acesso e você não pode construir uma Merkle para acessá-los também. Portanto, as árvores de Merkle são melhor usadas com algum tipo de armazenamento descentralizado, como IPFS.

Veja aqui mais do meu trabalho (opens in a new tab).

Última atualização da página: 18 de dezembro de 2025