Prove di Merkle per l'integrità dei dati offline

Introduzione

Idealmente, vorremmo archiviare tutto nell'archiviazione di Ethereum, memorizzata tra migliaia di computer e avente una disponibilità estremamente elevata (i dati non sono censurabili) e integrità (i dati non sono modificabili in un modo non autorizzato), ma archiviare una parola di 32 byte costa tipicamente 20.000 gas. Mentre scriviamo il presente articolo, tale costo equivale a 6,60 dollari. Ne consegue che 21 centesimi per byte sia un costo impraticabile per molti utilizzi.

Per risolvere questo problema l'ecosistema di Ethereum ha sviluppato molti metodi alternativi per memorizzare dati in modo decentralizzato. Solitamente occorre raggiungere un compromesso tra disponibilità e prezzo, mentre l'integrità è generalmente garantita.

In questo articolo imparerai come garantire l'integrità dei dati senza memorizzare i dati sulla blockchain, usando le prove di Merkle(opens in a new tab).

Come funziona?

In teoria, potremmo semplicemente memorizzare l'hash dei dati sulla catena e inviare tutti i dati nelle transazioni che lo richiedono. Anche questo però sarebbe troppo costoso. Un byte di dati per una transazione costa circa 16 gas, correntemente circa mezzo centesimo, o circa 5 dollari per kilobyte. 5.000 dollari per megabyte è un prezzo comunque proibitivo per molti utilizzi, anche senza il costo supplementare connesso all'hashing dei dati.

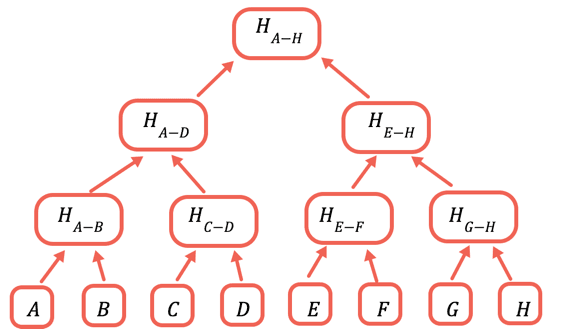
La soluzione consiste nel procedere ripetutamente all'hashing di diverse sottoserie di dati, quindi per i dati che non devono essere inviati è sufficiente inviare un hash. A tale scopo puoi utilizzare un albero di Merkle, una struttura di dati ad albero in cui ogni nodo rappresenta un hash dei nodi sottostanti:

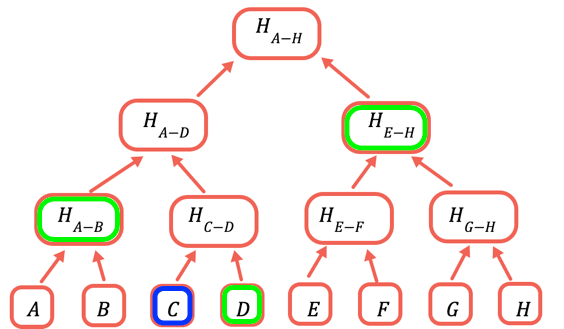
L'hash principale è l'unica parte che deve essere memorizzata sulla catena. Per provare un dato valore, occorre fornire tutti gli hash che devono essere combinati con esso per ottenere il root. Ad esempio, per provare C, occorre fornire D, H(A-B) e H(E-H).

Implementazione

Il campione di codice è disponibile qui(opens in a new tab).

Codice esterno alla catena

In questo articolo usiamo JavaScript per i calcoli al di fuori della catena. Gran parte delle app decentralizzate hanno i propri componenti esterni alla catena su JavaScript.

Creare il root di Merkle

Prima dobbiamo fornire il root di Merkle alla catena.

1const ethers = require("ethers")

Usiamo la funzione hash dal pacchetto ethers(opens in a new tab).

1// The raw data whose integrity we have to verify. The first two bytes a
2// are a user identifier, and the last two bytes the amount of tokens the
3// user owns at present.
4const dataArray = [
5  0x0bad0010, 0x60a70020, 0xbeef0030, 0xdead0040, 0xca110050, 0x0e660060,
6  0xface0070, 0xbad00080, 0x060d0091,
7]

Codificando ogni voce in un unico numero intero da 256 bit si ottiene un codice meno leggibile rispetto, ad esempio, all'utilizzo di JSON. Tuttavia, ciò comporta un'elaborazione significativamente ridotta per recuperare i dati nel contratto, quindi costi del gas molto inferiori. JSON può essere letto sulla catena(opens in a new tab), ma è una cattiva idea, quindi se possibile consigliamo di evitarlo.

1// The array of hash values, as BigInts
2const hashArray = dataArray

In questo caso, per iniziare i nostri dati sono valori da 256 bit, quindi non è necessaria alcuna elaborazione. Se usiamo una struttura di dati più complicata, come le stringhe, dovremo assicurarci di eseguire per prima cosa l'hashing dei dati, così da ottenere un insieme di hash. Anche questo, ricordiamo che non importa se gli utenti conoscono le informazioni altrui. In caso contrario, dovremmo eseguire l'hashing in modo tale che l'utente 1 non conosca il valore per l'utente 0, l'utente 2 non conosca il valore per l'utente 3, ecc.

1// Convert between the string the hash function expects and the
2// BigInt we use everywhere else.
3const hash = (x) =>
4  BigInt(ethers.utils.keccak256("0x" + x.toString(16).padStart(64, 0)))

La funzione hash di ethers prevede di ottenere una stringa in JavaScript con un numero esadecimale, come 0x60A7 e rispondere con un'altra stringa con la stessa struttura. Tuttavia, per il resto del codice è più facile usare BigInt, in modo da poter convertire in una stringa esadecimale e tornare indietro.

1// Symmetrical hash of a pair so we won't care if the order is reversed.
2const pairHash = (a, b) => hash(hash(a) ^ hash(b))

Questa funzione è simmetrica (hash di una b xor(opens in a new tab)). Questo significa che quando controlliamo la prova di Merkle, non dobbiamo preoccuparci di mettere il valore dalla prova prima o dopo il valore calcolato. Il controllo della prova di Merkle ha luogo sulla catena, quindi meno bisogna fare lì, meglio è.

Attenzione: La crittografia è più complessa di quanto sembri. La versione iniziale di questo articolo conteneva la funzione di hash hash(a^b). Quella era una cattiva idea, poiché comportava che, conoscendo i valori legittimi di a e b avresti potuto usare b' = a^b^a' per provare qualsiasi valore a' desiderato. Con questa funzione dovresti calcolare b' così che hash(a') ^ hash(b') sia pari a un valore noto (il ramo successivo verso la radice), il che è molto più difficile.

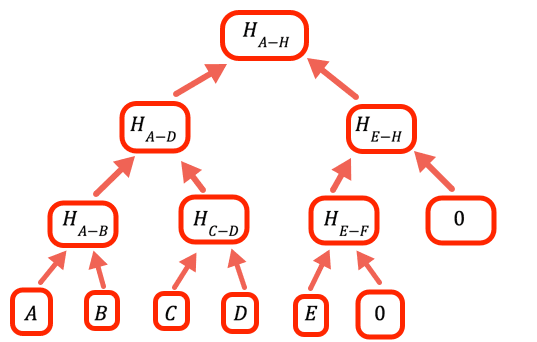
1// The value to denote that a certain branch is empty, doesn't
2// have a value
3const empty = 0n

Quando il numero di valori non è una potenza intera di due, dobbiamo gestire i rami vuoti. A tale scopo, questo programma inserisce zero come segnaposto.

1// Calculate one level up the tree of a hash array by taking the hash of
2// each pair in sequence
3const oneLevelUp = (inputArray) => {
4  var result = []
5  var inp = [...inputArray] // To avoid over writing the input // Add an empty value if necessary (we need all the leaves to be // paired)
6
7  if (inp.length % 2 === 1) inp.push(empty)
8
9  for (var i = 0; i < inp.length; i += 2)
10    result.push(pairHash(inp[i], inp[i + 1]))
11
12  return result
13} // oneLevelUp
Mostra tutto

Questa funzione "scala" un livello nell'albero di Merkle eseguendo l'hashing di coppie di valori al livello corrente. Nota che questa non è l'implementazione più efficiente: avremmo potuto evitare di copiare l'input e aggiungere semplicemente hashEmpty nel punto appropriato del ciclo, ma questo codice è ottimizzato per migliorare la leggibilità.

1const getMerkleRoot = (inputArray) => {
2  var result
3
4  result = [...inputArray] // Climb up the tree until there is only one value, that is the // root. // // If a layer has an odd number of entries the // code in oneLevelUp adds an empty value, so if we have, for example, // 10 leaves we'll have 5 branches in the second layer, 3 // branches in the third, 2 in the fourth and the root is the fifth
5
6  while (result.length > 1) result = oneLevelUp(result)
7
8  return result[0]
9}
Mostra tutto

Per ottenere la radice, scala finché non resta un solo valore.

Creare una prova di Merkle

Una prova di Merkle è data dai valori da sottoporre all'hashing insieme al valore dimostrato in modo da ottenere nuovamente il root di Merkle. Il valore da provare spesso è ricavabile da altri dati, quindi preferisco fornirlo separatamente anziché come parte del codice.

1// A merkle proof consists of the value of the list of entries to
2// hash with. Because we use a symmetrical hash function, we don't
3// need the item's location to verify the proof, only to create it
4const getMerkleProof = (inputArray, n) => {
5    var result = [], currentLayer = [...inputArray], currentN = n
6
7    // Until we reach the top
8    while (currentLayer.length > 1) {
9        // No odd length layers
10        if (currentLayer.length % 2)
11            currentLayer.push(empty)
12
13        result.push(currentN % 2
14               // If currentN is odd, add with the value before it to the proof
15            ? currentLayer[currentN-1]
16               // If it is even, add the value after it
17            : currentLayer[currentN+1])
18
Mostra tutto

Eseguiamo l'hashing di (v[0],v[1]), (v[2],v[3]), ecc. Quindi per i valori pari ci serve quello successivo, mentre per i valori dispari ci serve quello precedente.

1        // Move to the next layer up
2        currentN = Math.floor(currentN/2)
3        currentLayer = oneLevelUp(currentLayer)
4    }   // while currentLayer.length > 1
5
6    return result
7}   // getMerkleProof

Codice on-chain

Finalmente abbiamo il codice che verifica la prova. Il codice on-chain è scritto in Solidity(opens in a new tab). L'ottimizzazione è molto più importante qui, perché il gas è relativamente costoso.

1//SPDX-License-Identifier: Public Domain
2pragma solidity ^0.8.0;
3
4import "hardhat/console.sol";
 Copia

L'ho scritto usando l'ambiente di sviluppo Hardhat(opens in a new tab), che ci consente di avere l'output della console da Solidity(opens in a new tab) durante lo sviluppo.

1
2contract MerkleProof {
3    uint merkleRoot;
4
5    function getRoot() public view returns (uint) {
6      return merkleRoot;
7    }
8
9    // Extremely insecure, in production code access to
10    // this function MUST BE strictly limited, probably to an
11    // owner
12    function setRoot(uint _merkleRoot) external {
13      merkleRoot = _merkleRoot;
14    }   // setRoot
Mostra tutto
 Copia

Imposta e ottieni le funzioni per il root di Merkle. Consentire a chiunque di aggiornare il root di Merkle è un'idea assolutamente pessima in un sistema di produzione. Qui lo faccio per motivi di semplicità del codice di esempio. Sconsiglio di farlo su un sistema in cui l'integrità dei dati è importante.

1    function hash(uint _a) internal pure returns(uint) {
2      return uint(keccak256(abi.encode(_a)));
3    }
4
5    function pairHash(uint _a, uint _b) internal pure returns(uint) {
6      return hash(hash(_a) ^ hash(_b));
7    }
 Copia

Questa funzione genera l'hash di una coppia. È semplicemente la traduzione di Solidity del codice in JavaScript per hash e pairHash.

Nota: Questo è un altro caso d'ottimizzazione per migliorare la leggibilità. In base alla definizione della funzione(opens in a new tab), potrebbe essere possibile memorizzare i dati come valore bytes32(opens in a new tab) ed evitare le conversioni.

1    // Verify a Merkle proof
2    function verifyProof(uint _value, uint[] calldata _proof)
3        public view returns (bool) {
4      uint temp = _value;
5      uint i;
6
7      for(i=0; i<_proof.length; i++) {
8        temp = pairHash(temp, _proof[i]);
9      }
10
11      return temp == merkleRoot;
12    }
13
14}  // MarkleProof
Mostra tutto
 Copia

Nella notazione matematica, la verifica della prova di Merkle somiglia a questa: H(proof_n, H(proof_n-1, H(proof_n-2, ... H(proof_1, H(proof_0, value))...))). Questo codice la implementa.

Prove di Merkle e rollup non si mescolano

Le prove di Merkle non funzionano bene con i rollup. Il motivo è che i rollup scrivono tutti i dati della transazione su L1, ma elaborano su L2. Il costo medio per inviare una prova di Merkle con una transazione è di 638 gas per livello (correntemente, un byte nei dati della chiamata costa 16 gas se non è zero, e 4 se è zero). Se abbiamo 1024 parole di dati, una prova di Merkle richiede dieci livelli, o un totale di 6380 gas.

Ad esempio, guardando a Optimism(opens in a new tab), la scrittura del gas del L1 costa circa 100 gwei e del L2 circa 0,001 gwei (questo è il prezzo normale, può aumentare con la congestione). Quindi, per il costo di un gas del L1, possiamo consumare centomila gas sull'elaborazione del L2. Supponendo di non sovrascrivere l'archiviazione, ciò significa che possiamo scrivere circa cinque parole all'archiviazione sul L2, per il prezzo di un gas del L1. Per una singola prova di Merkle, possiamo scrivere tutte le 1024 parole all'archiviazione (supponendo innanzitutto che siano calcolabili sulla catena, piuttosto che fornite in una transazione) e comunque avere una rimanenza di gran parte del gas.

Conclusione

Nella vita reale potresti non trovarti mai a implementare alberi di Merkle per conto tuo. Esistono librerie ben note e controllate che puoi usare e, in generale, è meglio non implementare primitivi crittografici autonomamente. Ma spero che ora tu abbia compreso meglio le prove di Merkle e possa decidere quando vale la pena usarle.

Nota che benché le prove di Merkle preservino l'integrità, non preservano la disponibilità. Sapere che nessun altro può prendere le tue risorse è una magra consolazione se la memoria dati decide di non consentire l'accesso e non puoi neanche costruire un albero di Merkle per accedervi. Quindi gli alberi di Merkle funzionano meglio con qualche tipo di memoria decentralizzata, come IPFS.